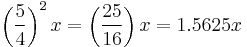Enharmonic

In modern musical notation and tuning, an enharmonic equivalent is a note (enharmonic tone) interval (enharmonic interval) or key signature (enharmonic key signature) which is equivalent to some other note, interval, or key signature but "spelled", or named differently (enharmonic relation). Thus, the enharmonic spelling of a written note, interval or chord is an enharmonic equivalent to the way that note, interval or chord would be written under the current key signature. In other words, if two notes have the same pitch but are represented by different letter names and accidentals, they are enharmonic. Enharmonic equivalence is not to be confused with octave equivalence, nor are enharmonic intervals to be confused with inverted or compound intervals. "Enharmonic equivalents are tones that have the same pitch but different letter names....Two tones having the same pitch but different spelling".^[1] "Enharmonic intervals are intervals with the same sound that are spelled differently...[resulting], of course, from enharmonic tones."^[2] Prior to this modern meaning, "enharmonic" referred to relations in which (using traditional notation) there is no exact equivalence between a sharpened note and the flattened note.^[3], as in enharmonic scale.

For example, in twelve-tone equal temperament (the currently predominant system of musical tuning in the West), the notes C♯ and D♭ are enharmonically equivalent—that is, they are the same key on a keyboard—and thus are identical in pitch, although they have different names and diatonic function, or role in harmony and chord progressions.

In a given diatonic scale, an individual note name may only occur once. In the key of F for example, the major scale is: 'F, G, A, B♭, C, D, E, (F)'. Thus, the 'B' is called 'B♭' rather than 'A♯' as we already have a note named 'A' in the scale. The scale of F♯ major is: 'F♯, G♯, A♯, B, C♯, D♯, E♯, (F♯)'; thus we use the term 'A♯' instead of 'B♭' as we need the name 'B' to represent the 'B' note in the scale, and 'E♯' instead of 'F' as we need the name 'F' to represent the 'F♯' note in the scale.

Some key signatures also have an enharmonic key signature that represents a scale identical in sound but spelled differently. The number of sharps and flats of enharmonic keys sum to twelve. For example, the key of B Major, with 5 sharps, is enharmonically equivalent to the key of C-flat major with 7 flats, and 5 (sharps) + 7 (flats) = 12. Keys past 7 sharps or flats exist only theoretically and not in practice. The enharmonic keys are six pairs, three major and three minor: B Major/C-flat Major, G-Sharp Minor/A-flat Minor, F-sharp Major/G-flat Major, D-sharp Minor/E-flat Minor, C-sharp Major/D-flat Major and A-sharp Minor/B-flat Minor. There are no works composed in keys that require double sharping or double flating in the key signature, except in jest. In practice, musicians learn and practice 15 major and 15 minor keys, three more than 12 due to the enharmonic spellings.

For example the intervals of a minor sixth on C, on B#, and an augmented fifth on C are all enharmonic intervals . The most common enharmonic intervals are the augmented fourth and diminished fifth, or tritone, for example C-F♯ = C-G♭.^[1]

1 Tuning enharmonics
- 1.1 Pythagorean
- 1.2 Meantone
2 Enharmonic genus
3 Enharmonic tetrachords in Byzantine music
4 See also
5 Sources
6 Further reading

Tuning enharmonics

In principle, the modern musical use of the word enharmonic to mean identical tones is correct only in equal temperament, where the octave is divided into 12 equal semitones; but even in other tuning systems enharmonic associations can be perceived by listeners and exploited by composers.^[4] This is in contrast to the ancient use of the word in the context of unequal temperaments, such as quarter-comma meantone intonation, in which enharmonic notes differ slightly in pitch. It should be noted, however, that enharmonic equivalents occur in any equal temperament system, such as 19 equal temperament or 31 equal temperament, if it can be and is used as a meantone temperament. The specific equivalences define the equal temperament. 19 equal is characterized by E♯ = F♭ and 31 equal by D = F, for instance; in these tunings it is not true that E♯ = F, which is characteristic only of 12 equal temperament.

Pythagorean

Main article: Pythagorean tuning

In Pythagorean tuning, all pitches are generated from a series of justly tuned perfect fifths, each with a ratio of 3 to 2. If the first note in the series is an A♭, the twelfth note in the series, G♯, will be higher than the seventh octave (octave = ratio of 1 to 2, seven octaves is 1 to 2⁷ = 128) of the A♭ by a small interval called a Pythagorean comma. This interval is expressed mathematically as:

$\frac{\hbox{twelve fifths}}{\hbox{seven octaves}} =\left(\tfrac32\right)^{12} \!\!\bigg/\, 2^{7} = \frac{3^{12}}{2^{19}} = \frac{531441}{524288} = 1.0136432647705078125 \!$

Meantone

Main article: Meantone temperament

In 1/4 comma meantone, on the other hand, consider G♯ and A♭. Call middle C's frequency $x$ . Then high C has a frequency of $2x$ . The 1/4 comma meantone has just (i.e., perfectly tuned) major thirds, which means major thirds with a frequency ratio of exactly 4 to 5.

In order to form a just major third with the C above it, A♭ and high C need to be in the ratio 4 to 5, so A♭ needs to have the frequency

$\frac {8x}{5} = 1.6 x. \!$

In order to form a just major third above E, however, G♯ needs to form the ratio 5 to 4 with E, which, in turn, needs to form the ratio 5 to 4 with C. Thus the frequency of G♯ is

$\left(\frac{5}{4}\right)^2x = \left(\frac{25}{16}\right)x = 1.5625 x$

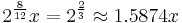Thus, G♯ and A♭ are not the same note; G♯ is, in fact 41 cents lower in pitch (41% of a semitone, not quite a quarter of a tone). The difference is the interval called the enharmonic diesis, or a frequency ratio of $\frac{128}{125}$ . On a piano tuned in equal temperament, both G♯ and A♭ are played by striking the same key, so both have a frequency $2^\frac{8}{12}x = 2^\frac{2}{3} \approx 1.5874 x$ . Such small differences in pitch can escape notice when presented as melodic intervals. However, when they are sounded as chords, the difference between meantone intonation and equal-tempered intonation can be quite noticeable, even to untrained ears.

The reason that — despite the fact that in recent Western music, A♭ is exactly the same pitch as G♯ — we label them differently is that in tonal music notes are named for their harmonic function, and retain the names they had in the meantone tuning era. This is called diatonic functionality. One can however label enharmonically equivalent pitches with one and only one name, sometimes called integer notation, often used in serialism and musical set theory and employed by the MIDI interface.

Enharmonic genus

Main article: Enharmonic genus

In ancient Greek music the enharmonic was one of the three Greek genera in music in which the tetrachords are divided (descending) as a ditone plus two microtones. The ditone can be anywhere from 16/13 to 9/7 (3.55 to 4.35 semitones) and the microtones can be anything smaller than 1 semitone. Some examples of enharmonic genera are

1. 1/1 36/35 16/15 4/3

2. 1/1 28/27 16/15 4/3

3. 1/1 64/63 28/27 4/3

4. 1/1 49/48 28/27 4/3

5. 1/1 25/24 13/12 4/3

Enharmonic tetrachords in Byzantine music

In Byzantine music, enharmonic describes a kind of tetrachord and the echos that contain them. As in the ancient Greek system, enharmonic tetrachords are distinct from diatonic and chromatic. However Byzantine enharmonic tetrachords bear no resemblance to ancient Greek enharmonic tetrachords. Their largest division is between a whole-tone and a tone-and-a-quarter in size, and their smallest is between a quarter-tone and a semitone. These are called "improper diatonic" or "hard diatonic" tetrachords in modern western usage.

Sources

^ ^a ^b Benward & Saker (2003). Music in Theory and Practice, Vol. I, p.7 & 360. ISBN 978-0-07-294262-0.
^ Benward & Saker (2003), p.54.
^ Louis Charles Elson (1905) Elson's Music Dictionary, p.100. O. Ditson Company. "The relation existing between two chromatics, when, by the elevation of one and depression of the other, they are united into one".
^ Rushton, Julian (2001). "Enharmonic", The New Grove Dictionary of Music and Musicians. Second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers. ISBN 0195170679.